| A0 841X1189 |
A1 594X841 |
A2 420X594 |
A3 297X420 |
A4 210X297 |
A5 148X210 |
A6 105X148 |
A7 74X105 |
A8 52X74 |
A9 37X52 |
A10 26X37 |
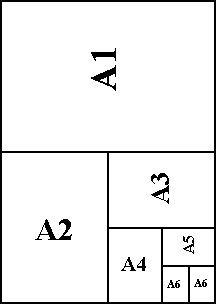 The figure to the right represents a sheet of A0 paper, whose area
is defined as one square meter (106 square millimeters). If
the dimensions of A0 in millimeters are W (Width) and H (Height), we
have...
The figure to the right represents a sheet of A0 paper, whose area
is defined as one square meter (106 square millimeters). If
the dimensions of A0 in millimeters are W (Width) and H (Height), we
have...
WH = 106
The goal is for an A1 sheet to be half of an A0 (and for an A2 to be half of an A1, ktp), with all sizes having the same aspect ratio (width/height). So if W and H are the dimensions for any particular size, then its aspect ratio is W/H, and the aspect ratio for the next smaller size is (H/2)/W, and these aspect ratios are the same...
W/H = (H/2)/W
Solving both equations for W2 and equating the results...
(H2)/2 = (1012)/H2
H4 = (2)(1012)
H = 1189 (to the nearest integer)
And...
W = 106/H = 841 (to the nearest integer)
Thus may the dimensions of A0 paper, and consequently the dimensions of the other sizes in the A series, be determined.
P.S. A4 is approximately the size of Usonian 8.5X11.